Cross-posted from the ROOT blog where this post first appeared.
ROOT comes with support for different pseudorandom number generators (PRNGs). This post discusses the recent implementation of RANLUX++ and how I tuned its performance. Because of its theoretical strengths and its performance, this generator might become the default in future versions of ROOT.
The added TRandomRanluxpp joins the group of available RNGs in ROOT:
TRandom1is the RANLUX generator proposed by Martin Lüscher. The implementation is based on the original description by Fred James and generates single precision values based on 24 bits of randomness.TRandom3is based on the Mersenne Twister generator. By default, this implementation is used forgRandomand generates 32 bits of randomness.TRandomMixMaxis a 61 bits matrix recursive MIXMAX generator (described in https://mixmax.hepforge.org/). It is based on a state of size 240, other sizes are available viaMixMaxEngine.
There are a few more variants that are linked in the documentation.
Why so many PRNGs?
There exist many properties to evaluate PRNGs, with the easiest being its period: it captures how many random numbers can be generated before the sequence “wraps around” and repeats. For obvious reasons, the period of a PRNG cannot be longer than its state. This is one of the problems of the oldest LCGs with a state of 32 bits or less.
However, there are many more statistical properties that are at least equally important. A widely used collection of empirical tests is TestU01 by L’Ecuyer and Simard. It has to be noted that the tests can only prove the existence of defects. That is, passing all tests does not mean that a PRNG is free of errors.
As with many other design issues, PRNGs need to make a certain trade-off: fast generators with a small state will usually fail many statistical tests. On the other hand, good generators are typically slower or use a much larger state. In fact, most generators will fail one test or another, including the widely used Mersenne Twister. Notable exceptions are RANLUX and MIXMAX that pass all currently known tests.
RANLUX++
RANLUX++ is an LCG implementation derived from the ideas of RANLUX. It aims to provide better performance while maintaining the good properties of RANLUX. In particular, this includes the foundation based on mixing of classical mechanical systems. For this reason, the randomness of the generated sequence can be theoretically understood. The formulation as LCG makes it possible to reach even better properties without impact on performance.
The generator uses a single 576 bit number as state. When invoked, it hands out the next unused bits that the generator remembers as an offset. Once all bits are exhausted, the LCG performs a multiplication and a modulo operation to advance the state. Arithmetic on 576 bit numbers is way beyond what current hardware offers. Instead the state is portably stored as 9 numbers of 64 bits each. On this representation, multiplication and the modulo operation must thus be done in software. For the multiplication, this is very similar to the way multiplications are taught in high school. The modulo operation can take advantage of the known modulus (for details, refer to section 2.1 of the paper).
For efficiency reasons, Sibidanov implemented the routines in x86 assembly. This results in impressive performance, but it is not portable across all architectures supported by ROOT. So how much slower would a portable implementation be? After implementing RANLUX++ for ROOT, it turns out: not much!
The initial version added to ROOT takes around 30ns per random double sampled.
For comparison, the implementation by Sibidanov comes in at around 8ns per number.
This was measured with 10 repetitions of a microbenchmark with a standard deviation of less than 1%.
The numbers are from a single core of an AMD Ryzen 9 3900 running CentOS 8.2.2004.
The default compiler is GCC in version 8.3.1, but I will present more numbers in the following.
Performance tuning
30ns per number is already quite impressive and twice as fast compared to TRandom1.
That implementation of RANLUX takes around 62ns per number and only generates single precision values.
It must be noted that a newer version by Lüscher was also measured at 30ns for double values.
That said, can we do even better? Yes!
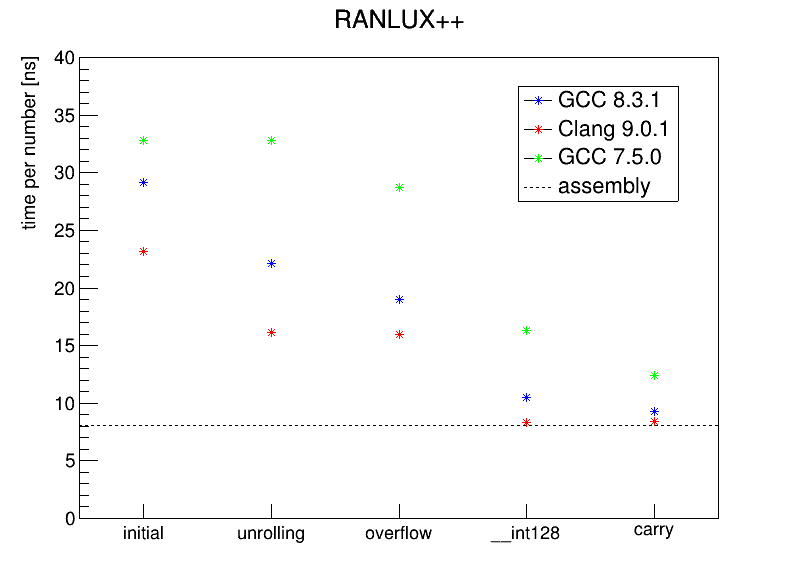
The graph below shows the evolution of performance after tuning. In addition to GCC 8.3.1, I also include numbers for Clang 9.0.1 and GCC 7.5.0. While the former two are packaged for CentOS 8, I compiled GCC 7.5.0 from the official sources. The dashed horizontal line represents the assembly version by Sibidanov. Details about the individual changes are described in the following sections.
Loop unrolling
The portable code relies on loops to implement the multiplication and modulo operation in software. This induces overhead when evaluating the exit condition and incrementing the loop variable. Furthermore, the loop structure leads to jumps in the code that hinder instruction level parallelism. Fortunately loop unrolling is a well known compiler optimization to tackle this problem: it duplicates the loop body to enable other optimization passes and generate more efficient code. In case of constant loop bounds, it is even possible to fully unroll the loop.
One disadvantage of loop unrolling is the increased code size.
For this reason, compilers are conservative in their unrolling heuristics.
During experiments, I found that unrolling of certain loops consistently improves performance.
By adding #pragma directives, it is possible to help the compiler.
As can be seen in above graph, this improves performance for GCC 8.3.1 and Clang 9.0.1 by up to 30%.
GCC 7.5.0 does not benefit from the change because #pragma GCC unroll was only added in GCC 8.
Overflow handling
For the multiplication of two 576 bit numbers, the portable code is constrained by the available data types:
it can at most multiply two 32 bit values at a time to stay within the 64 bits of uint64_t.
This makes it necessary to handle overflows when summing up the partial results.
By arranging the operations differently, it is possible to avoid conditional execution.
Together with full unrolling, this eliminates all jumps from the generated machine code for GCC 8.3.1.
During execution, this leads to performance improvements of up to 15% for the two versions of GCC.
There is no change for Clang because its optimizations already transformed the original code.
Native multiplication
An even faster way is to let hardware handle the multiplication of two 64 bit numbers.
This is possible with the extension type __int128 supported by both GCC and Clang.
Using this type, it is possible to multiply 64 bit numbers with 128 bit precision.
For that, the compiler can make use of special instructions available for the targeted hardware.
Afterwards the upper and lower halves can be extracted as 64-bit numbers.
The change taking advantage of __int128 improves performance of all three compilers by more than 40%!
Carry propagation
Additional tests showed inferior performance with older compilers.
Part of this is related to missing loop unrolling because the #pragma is not available (see above).
An additional problem is the generation of jumping code to propagate carry bits in case of overflows.
Instead of relying on inline assembly code, I found a portable solution after refactoring the common code.
The modification results in good code for all tested compilers.
For the older GCC 7.5.0 in particular, it improves performance by more than 20%.
Conclusion
In this blog post, I discussed the implementation of RANLUX++ and its performance.
After tuning, the average time per number is down to around 9ns, very close to the assembly version.
It is slightly slower than TRandom3 currently used for gRandom (around 3ns per number).
However, TRandom3 generates 32 bits of randomness while TRandomRanluxpp uses 52 bits per double value.
Furthermore RANLUX++ inherits and extends the mathematically proven properties of RANLUX.
As it also passes all tests in TestU01, it might replace the default gRandom in the future.
But you do not need to wait until then: TRandomRanluxpp will be available with version 6.24 of ROOT.
Once released, you can replace the default generator as described in the documentation.
Or use a nightly version right now via LCG or Conda!
You do not need to agree with my opinions expressed in this blog post, and I'm fine with different views on certain topics. However, if there is a technical fault please send me a message so that I can correct it!